テレビを見ていたら、平野が丁寧のドライブを前陣でカウンターする様子を横方向から映した画像が流れた。
コマ送りをしてみると、ラケットの角度、ボールの軌跡、スイングの方向がうまいぐあいにわかるような画像だったので、測定してみた。
すると、ラケットの角度はボールの軌道に対して43.5度、スイング方向は46度だった。つまり、飛んでくるボールに対して約45度の方向にほとんど面の方向にスイングしているのだ。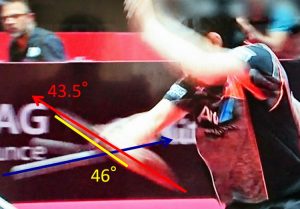
これはとんでもなく困難なことだ。
どういうことか。この映像はスロー再生だったし露出時間もわからないのでスイングの速さは正確にはわからないが、これまでの他の測定からだいたい時速30km程度だと思われる。これは秒速8.3mだ。ということは、0.01秒間に8cmの速さでボールの軌道を45度の角度で横切る打ち方をしていることになる。
ラケットの幅は約15cmだから、約0.02秒の誤差しか許されない正確さでスイングしなくてはラケットに当たらないということなのだ。当たるといっても、端に当たったのでは入らないのだから、実際にはその半分程度の誤差しか許されないだろう。
なぜ普通に真っ直ぐ当てないで、こんな空振りスレスレの打ち方をするかといえば、回転をかけたいからだ。激しい前進回転がボールの軌道を丸め、ネットを越した後に台に入ることに役立つからだ。遅いボールなら回転などかけなくても重力で落ちてくれるので台に入るが、なにしろ丁寧の反応時間を破るほどのスピードのボールを打たねばならないのだから、回転をかけなかったらボールは真っ直ぐに飛んでいって台に入ってくれない。
速いボールを台に入れるために激しい前進回転がどうしても必要なのだ。
どこにくるかわからない相手のボールのコースと回転量を判断してラケットの角度を出して0.02秒の誤差で振り抜く。そんなこと人間にできるのだろうか。
できるから平野はやっているわけだ。そして、ひとりができてそれが可能であることを示すと、他の選手もどんどんできるようになるのがスポーツの常だ。
まったく凄い世界だ。
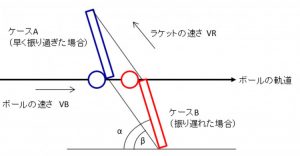
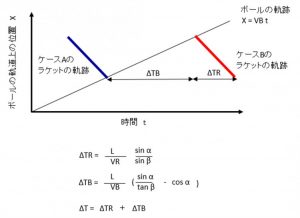
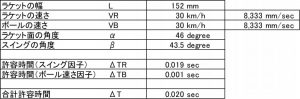
ちなみに、面の方向とスイングの方向が2.5度違っているわけだが、その影響も考慮して許容誤差時間を真面目に計算すると、0.020秒となった。なお、ボールの速さは時速30km、ラケットの幅は152mmとした。
説明は省略するが、暇な人は眺めて見てほしい。
そのうち、きちんとスーパースローカメラで真横から撮影して正確な測定をしてみたいものだ。ああ面白い。

出ましたね。条太さんの真骨頂!
当然ながら、凡人には全然わかりませんが…